Matematica e Fisica: STORIA DELLA TRIGONOMETRIA: ANGOLI E TRIGONOMETRIA DEGLI ANTICHI EGIZI

ANGOLI E TRIGONOMETRIA DEGLI ANTICHI EGIZI

-GONIOMETRIA E TRIGONOMETRIA

La goniometria è la branca della matematica che si occupa della misura degli angoli e delle funzioni associate,mentre la trigonometria(etimologia: dal greco trigonon e metron) è una branca della matematica che si occupa di stabilire le relazioni che intercorrono tra la lunghezza dei lati e l’ampiezza degli angoli di triangoli piani (trigonometria piana) o sferici (trigonometria sferica). Per triangolo sferico si intende una figura costruita sulla sfera delimitata da tre archi di cerchio massimo, che abbiano cioè raggio pari a quello della sfera. L'identità fondamentale della goniometria e trigonometria si verifica con il teorema di Pitagora.Le relazioni che intercorrono tra angoli e lati dei triangoli sono definite con l'ausilio di determinate funzioni dette goniometriche o trigonometriche. Le quattro funzioni fondamentali di un angolo “α” sono:

1) il seno(sin α), il rapporto tra il cateto opposto all'angolo e l'ipotenusa= l'inversa della funzione seno è la cosecante (csc α )= la funzione inversa è l'arcoseno( sin^-1).

2) il coseno (cos α), il rapporto tra il cateto adiacente all'angolo e l'ipotenusa= l'inversa della funzione coseno è la secante (sec α)= la funzione inversa è l'arcocoseno (sen^-1).

3) la tangente(tan α), il rapporto tra il cateto opposto all'angolo e quello adiacente= l'inversa della funzione tangente è la cotangente (cot α)= la funzione inversa è l'arcotangente( tan^-1).

-NEGLI ANTICHI EGIZI

Le testimonianze degli storici greci (Erodo) vogliono che la geometria (letteralmente misura della terra) sia nata in Egitto e che i primi geometri dell’antichità siano gli agrimensori (geometria significa letteralmente misura della terra e la sua conseguente suddivisione). I greci danno loro il nome di arpedonapti, annodatori di corde. Tirando le funi, questi potevano tracciare sul terreno rette (tendendo una fune tra due punti) e cerchi (facendo ruotare un punto attorno ad un altro che rimane fisso), operazione utilizzata per diretti scopi pratici nella vita quotidiana (agricoltura, commercio, uso del calendario). Inoltre già nella prima dinastia erano diffuse la pratica della misurazione del livello di acqua del Nilo, e il rituale del “tendere la corda” per la costruzione dei templi, tra cui le piramidi, a conferma dell’uso di nozioni geometriche (da qui l'espressione "tirare una retta"). Il papiro di Rhind (o Ahmes, nome dello scriba che lo trascrisse verso il 1650 a.C) è il più esteso e antico papiro egizio di natura matematico-geometrica giunto fino a noi. Contiene tabelle di frazioni e 84 problemi aritmetici, algebrici e geometrici con le relative soluzioni, formule per aree (ad esempio l'area di un triangolo isoscele viene calcolata dividendolo in due triangoli rettangoli e ruotandone uno in modo da ottenere un rettangolo. Si trova il risultato, quindi, moltiplicando la metà della base per l'altezza) e procedimenti di moltiplicazione, divisione e operazioni con frazioni a numeratore unitario, media aritmetica, media geometrica, media armonica e numeri perfetti, oltre ad un metodo per la risoluzione lineare di equazioni di primo grado.

Papiro di Rihind

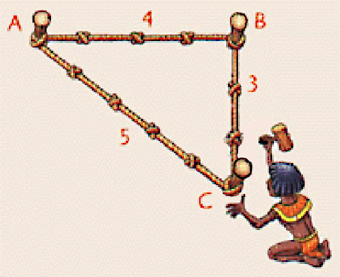
Gli antichi Egizi utilizzavano inoltre un articolato sistema di unità di misura per grandezze fisiche come lunghezza, superficie, volume e peso. Ciascuna unità di base possedeva un sistema di multipli e di sottomultipli. La loro perfetta applicazione è spiegabile dal fatto che possedevano una comprensione dei principi alla base del teorema di Pitagora o meglio del suo inverso, e cioè la consapevolezza del fatto che un triangolo i cui lati hanno lunghezza 3, 4 e 5, nel quale quindi il quadrato del lato maggiore è uguale alla somma dei quadrati degli altri due, ha un angolo retto di fronte all’ipotenusa. Disponendo allora di una corda ad anello, di lunghezza totale 12, sulla quale siano segnati tre punti, a distanze per l'appunto 3, 4 e 5, e tirandola a forma di triangolo con i vertici nei punti segnati, si ottiene un angolo retto. Nessun altro angolo oltre a questo possiede questa proprietà di simmetria.Angoli di 90° servivano per tracciare il perimetro alla base delle piramidi. La tipologia costruttiva dell'Antico Egitto si basa sulla scelta di una piramide a base quadrata e facce laterali uguali. Il

caso per eccellenza è costituito dalla piramide di Cheope, edificata tra il 2500 e il 2400 a.C.; lo storico Erodoto riferisce nelle Storie, di un particolare accorgimento dettato dai sacerdoti egiziani che volevano l’area di ogni faccia triangolare pari a quella del quadrato avente per lato l’altezza della piramide stessa, misurata a piombo dall’apice del monumento sino al terreno. L’equazione imposta dai sacerdoti sarebbe dunque b^2= ac, b è l’altezza della piramide.